Acte
La coupure est l’acte qui instaure le sujet en le divisant. Elle est un acte, car elle a cet effet décisif « d’instauration ».
L’acte de coupure s’applique au réel du sujet, celui de l’objet petit a — ou bien celui du sujet antérieur S, lors de la « première opération interrogative » dans une antériorité logique. En divisant le réel, la coupure délivre un signifiant qui représente le sujet dans le champ de l’Autre : Lacan l’appelle le « signifiant S1 ». Simultanément, Lacan appelle S2 « un autre signifiant » auquel s’adresse le signifiant S1 « qui représente le sujet ».
Création du savoir
La répétition de la coupure signifiante génère de nouveaux signifiants S1. Par extension, « S2 » dénote le savoir, c’est-à-dire l’addition des autres signifiants qui sont déjà là, l’accumulation des signifiants S1 qui viennent s’ajouter au savoir. À la différence de la vérité qui est l’effet du réel, le savoir est l’effet d’une collection de signifiants qui s’articulent en formant des phrases, des livres, des films, des symphonies ou des chansons, des tableaux, des théorèmes, des constitutions, des contrats d’affaires, etc., c’est-à-dire des histoires, des récits, des fresques, des théories, de la fiction, de la politique, des échanges commerciaux. C’est tout ce que l’être humain a produit et continue de produire dans l’ordre symbolique.
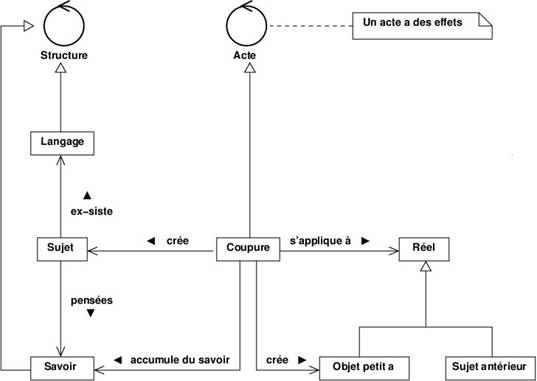
Acte de coupure
Références
Séminaire 10 : [page 189] […] le sujet fait une première opération interrogative dans le grand A — combien de fois ? […] le petit a en tant qu’il est justement ce qui représente le S [l’être du sujet] dans son réel irréductible […]
Séminaire 14 : [séance du 15/02/1967] Mais comment définir ce qu’est un acte ? Il est impossible de le définir autrement que sur le fondement de la double boucle, autrement dit de la répétition. Et c’est précisément en cela que l’acte est fondateur du sujet […] Le sujet, disons dans l’acte est équivalent à son signifiant. Il n’en reste pas moins divisé.
Séminaire 14 : [séance du 22/02/1967] Il [l’acte] est instauration du sujet comme tel. C’est-à-dire que d’un acte véritable le sujet surgit différent : en raison de la coupure sa structure est modifiée.
Séminaire 14 : [séance du 07/06/1967] Un acte […] n’a pas besoin d’être pensé, pour être un acte. La question se soulève même, de savoir si ce n’est pas pour ça qu’il est un acte ! […] mais il est certain […] qu’on ne peut le penser qu’après !
Séminaire 16 : [page 311] Il s’agit du rapport premier, mais gros de tous les autres, de S1 à S2, du signifiant qui représente le sujet pour un autre signifiant.
Séminaire 17 : [pages 11-12] […] nous considérons S1 et, désignée par le signe S2, la batterie des signifiants. Il s’agit de ceux qui sont déjà là […] S1 est celui qui est à voir comme intervenant. Il intervient sur une batterie signifiante que nous n’avons aucun droit, jamais, de tenir pour dispersée, pour ne formant pas déjà le réseau de ce qui s’appelle un savoir.
Séminaire 17 : [page 20] […] le champ propre de l’esclave, c’est le savoir, S2 […] ce que j’avance de l’esclave comme caractérisé par être celui qui est le support du savoir ne fait aucun doute.
Arithmétique
Congruence en arithmétique modulaire
En arithmétique modulaire, on dit qu’un entier a est congru à un entier b modulo n lorsque leur division par n donne le même reste. Par exemple, 9, 16, 23, 30, etc. sont congrus à 2 modulo 7 : le reste de la division entière par 7 est toujours 2. La congruence établit une relation d’équivalence sur l’ensemble des entiers : chaque nombre entier est congru à son reste, donc tous les membres d’une classe de congruence sont équivalents au reste, et le reste les représente tous. Dans l’exemple donné, les nombres cités et l’infinité de ceux qui suivent modulo 7 sont tous congrus à 2 : ils peuvent tous être représentés par l’entier 2 dans l’ensemble fini des entiers modulo 7 comprenant les 7 éléments {0, 1, 2, 3, 4, 5, 6}. Cela permet de faire de l’arithmétique sur des ensembles finis, puisque chaque valeur du modulo détermine une partition — qui est un ensemble fini — de l’ensemble infini des nombres entiers. Dans notre exemple, n’importe quel élément de l’ensemble des nombres entiers est congru à un et un seul des éléments de la partition modulo 7 : {0, 1, 2, 3, 4, 5, 6}, c’est-à-dire au reste de sa division entière par 7.
La métonymie est équivalente à la congruence : c’est un déplacement dans un espace fini. Tout déplacement dans un espace fini est nécessairement une répétition, parce qu’aucune incrémentation ou décrémentation ne permet de sortir de l’intervalle [0, (modulo-1)] : par exemple, dans l’ensemble ci-dessus des entiers modulo 7, l’incrémentation de 6 (l’opération 6+1) ne donne pas la valeur 7 mais la valeur 0, et ainsi de suite éternellement.
Congruence des objets petit a
Par l’effet de la congruence et de la notion de reste, tous les objets petit a résultant des divisions successives sont équivalents entre eux : quel qu’il soit au fil des divisions, chaque objet petit a est toujours le reste réel du sujet.
Il y a congruence entre l’être du sujet et l’objet petit a : le sujet demeure attaché au réel de son corps concret, c’est-à-dire au reste, à l’objet petit a. Pendant ce temps, « le sujet barré vit sa vie » et s’ébroue à son aise en tant qu’avatar dans l’univers des signifiants.
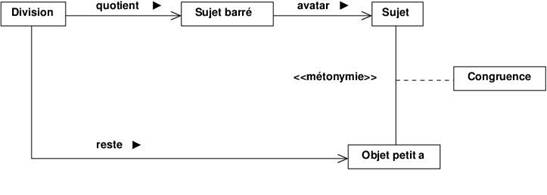
Division en arithmétique entière
Références
Séminaire 10 : [page 37] Par rapport à l’Autre, le sujet dépendant de cet Autre s’inscrit comme un quotient […] Il y a, au sens de la division, un reste, un résidu. Ce reste […] c’est le petit a.

Merci très instructif, mais très difficile; peut-être une traduction serait la bienvenue
Bonjour et merci,
Pouvez-vous préciser en quoi cela est difficile? En fait, cela n’est simplement que la division en arithmétique entière avec un quotient et un reste, extrapolée au niveau du sujet.
Merci encore